A regular hexagon is inscribed in a circle and another regular hexagon is circumscribed about the same circle. What is the ratio of the area of the larger hexagon to the area of the smaller hexagon? Express your answer as a common fraction.
How is this done? Would we divide it into triangles?
Thanks a lot for helping.
drwls you were close it's 4/3
It is 4/3.
4/3 is the answer.
KEJNHBGLVJH<SD
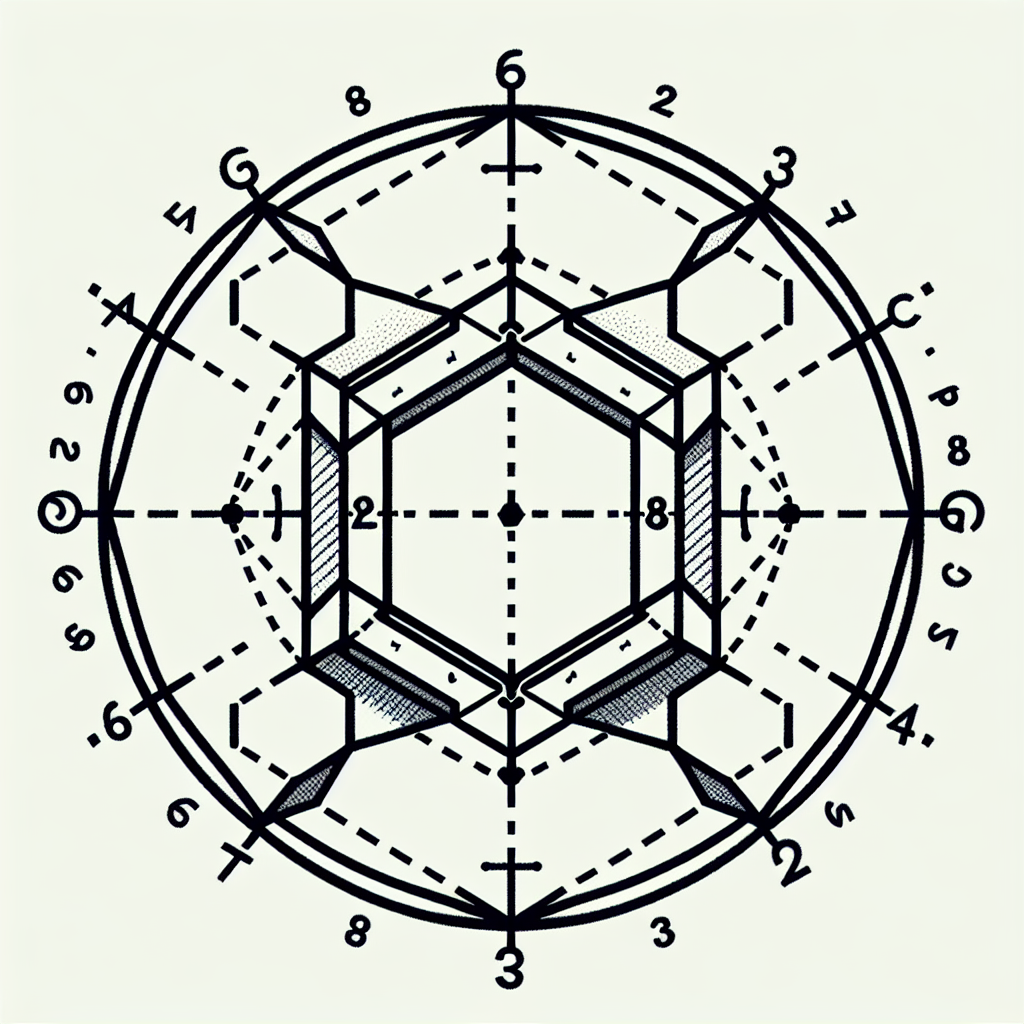
Form a triangle whose first vertex is the center of the circle and whose other two vertices are the midpoint and one of the endpoints of a side of the larger hexagon, as shown in the diagram. Since each interior angle of a regular hexagon is 120 degrees, this triangle is a 30-60-90 right triangle. Let $r$ be the radius of the circle. The length of the longer leg of the triangle is $r$, so the length of the shorter leg is $r/\sqrt{3}$ and the length of the hypotenuse is $2r/\sqrt{3}$. Since for the smaller hexagon the length of the segment connecting a vertex to the center is $r$, the dimensions of the larger hexagon are $2/\sqrt{3}$ times larger than the dimensions of the smaller hexagon. Therefore, the area of the larger triangle is $(2/\sqrt{3})^2=\boxed{4/3}$ times greater than the area of the smaller triangle.
[asy]
size(5cm);
defaultpen(linewidth(.7pt)+fontsize(8pt));
dotfactor=4;
int i;
draw(circle((0,0),1));
for(i=0;i<=5;++i)
{
draw(dir(60*i)--dir(60*(i+1)));
draw(2/sqrt(3)*dir(60*i)--2/sqrt(3)*dir(60*(i+1)));
}
draw(2/sqrt(3)*dir(0)--(0,0)--dir(30));
draw(0.93*dir(30)--dir(30)+0.07*dir(-60)+0.07*dir(210)--dir(30)+0.07*dir(-60));[/asy]
yo i need help
Realize that a hexagon is six equilateral triangles stacked together. You need the radii if the inscribed and circumscribed circles. The area ratio is the square of the ratio of those two radii.
The circumscribed circle radius is the side length of the equilateral triangles. Call that a. The inscribed circle has a radius that is the height of the equilateral triangles, a*sqrt3/2
The square of the radius ratio is 3/4