Homework Help: calculus

Posted by erico on Thursday, September 20, 2012 at 6:08am.

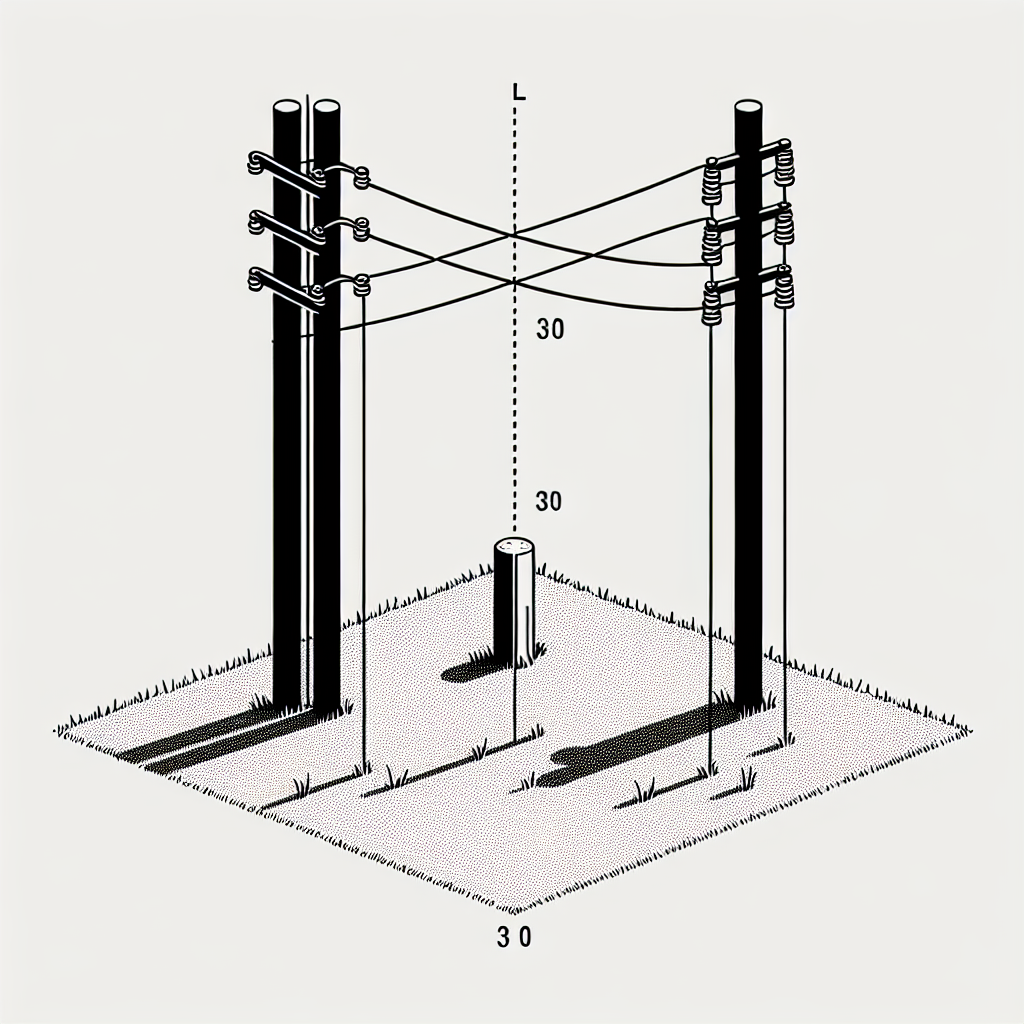
2 posts one is 10m high and other is 15m higs stand 30m apart they are to be stayed by transmission wire attached to a single stake at the ground level, the wire running to the top of the post , where should stake place to used least amount of wire ?

calculus - Reiny, Thursday, September 20, 2012 at 8:07am
simplest way:

draw a parallelogram ABCD, where AB = 10 (first post)
CD = 15 (2nd post) and BC = 30
Reflect AB in the line BC to point A1 , so that AB= BA1
joint DA1 intersecting BC at P

length of wire = AP+DP = A1P+DP , which is a straight line, and the shortest distance between two points is a straight line, ahhhhh....

let BP=x
Triangles ABP and A1PB are congruent, thus AP=A1P.
Also angles BPA1 and CPD are opposite, thus equal, making triangles APB and DPC similar

Therefore:
x/10 = (30-x)/15
15x = 300-10x
25x=300
x = 12

Put stake 12 m from the 1st post
calculus - Reiny, Thursday, September 20, 2012 at 8:24am
In the above solution, the actual calculation consists of the last 4 lines, the rest explains why it works

otherwise .... CALCULUS

AP^2 = x^2 + 10^2
AP = √(x^2 + 100)

PD^2 = (30-x)^2 + 15^2
PD = √(x^2 - 60x + 1125)

L = √(x^2 + 100) + √(x^2 - 60x + 1125)
= (x^2 + 100)^(1/2) + (x^2 - 60x + 1125)^(1/2)

dL/dx = (1/2)(x^2 + 100)^(-1/2) (2x) + (1/2)(x^2 - 60x + 1125)^(-1/2) (5x - 60)
= 0 for a min of L

x/√(x^2 + 100) = -(x-30)/√(x^2 - 60x + 1125)
square both sides

x^2/(x^2 + 100) = (x^2 - 60x + 900)/(x^2 - 60x + 1125)
cross multiply
x^4 - 60x^3 + 900x^2 + 100x^2 - 6000x + 90000 = x^4 - 60x^3 + 1125x^2
125x^2 + 6000x - 90000=0
x^2 + 48x - 720 = 0
(x-12)(x+60) = 0
x = 12 or x = -60 , but x can't be negative, so

x = 12

Answer this Question

Related Questions

Calculus - Two posts, one 12 feet high and the other 28 feet high, stand 30 feet...
Calculus - Two posts, one 12 feet high and the other 28 feet high, stand 30 feet...
Physics - An objectis thrown upward from the edge of a tall building with a ...
math - charlie is designing an 80 ft by 120ft rectangular fence. he wants to put...
chem - im studying for a test and i have no idea where to even start for this ...
Physics - A mass is dropped from a height of 30m, and at the same time from ...
physics - A mass is dropped from a height of 30m, and at the same time from ...
physics - A 1000kg rocket is moving forward at 10m/s in space. A 10,000N force ...
physics - a box slides down a smooth inclined plane 30m long and 10m high....
physics - A mass is dropped from a height of 30m, and at the same time from ...

For Further Reading

First Name:
School Subject:
Answer: